PHP 中的树和树遍历
我将在本文中介绍树结构。什么是树,如何使用以及何种情况下使用、
请注意,这只是一个基本的介绍,而不是整个故事。我甚至可能在某个地方错了,如果你认为我搞错了:请在评论中告诉我,或者给我发私信。
🌳 什么是树?
要回答这个问题,我们首先要看一下图(Graph)。在图论中,图(Graph)是以某种方式相互关联的数据点(或节点 Node)的(视觉)结构。例如,这种关系可以是有子节点或兄弟节点的父节点。这些节点(Node)之间的关系由一条线/顶点(或边)表示。在“正常”图形中,这些关系可以遍布各处。每个节点都可以连接到另一个甚至多个节点。边缘可以在任何地方弯曲。
那么什么是树呢?它是 Graph 的一个子集,只允许任何两个节点通过一条路径连接,而不是无限路径连接。
图(Graph) vs. 树(Tree)
比如:父节点 Parent 有两个子节点: Child 1 和 Child 2,图 Graph 允许有这些关系:
Parent <-> Child 1Parent <-> Child 2Child 1 <-> Child 2
这也被称为循环图( cyclic graph),因为它有一个循环(多个节点连接到相同的节点,在表示中创建循环)。
注意:图不一定有循环,但可以是。
而树(Tree)只允许像这样的关系:
Parent <-> Child 1Parent <-> Child 2
或者:
Parent <-> Child 1Child 1 <-> Child 2
一幅画胜过千言万语;让我们看一个(简单的)图形与树。
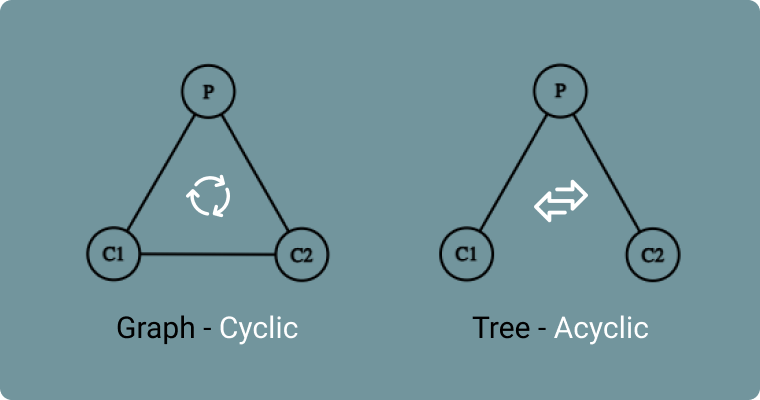
请注意,在树中,每对节点只通过一条边连接,因此永远不会有任何循环。这就是为什么树是非循环图(acyclic graphs)的原因。
什么元素组成一棵树呢?
正如我们在上图中看到的,树的顶部总是有一个节点。这称为根节点(Root Node)。
节点(Node)可以有值,但不强制要求。 它可以有、也可以没有子节点。一个节点如果没有子节点,可以称之为叶子(Leaf) 🍃 .
任何节点都可以有多个子节点,但有些树只允许每个节点有最大数量的子节点。这些被称为 N 元树(N-ary Trees),其中 N 表示每个节点的最大子级数量。可能这些树类型中最著名的是二进制树,它只允许2个子节点;左(left)和右(right)。
关于树的结构还有很多要讲的,但需要基本的理解;这应该足够了。让我们继续行动吧!
🚶 遍历树
树作为一种视觉展示很好,不过你也可以遍历树的完整结构并使用每个节点的数据。当遍历一棵树时,我们会访问树中的每个节点一次。而访问只是一个“在此执行操作”的代词。这个操作可以是任何你想要的:打印、保存或更改。无论你想对节点做什么,每次遍历每个节点都可以访问一次。
遍历一棵树有很多方法。你可以 Zig-zag,随意挑选一个顺序;但树遍历有两种广谱类型:深度优先和宽度优先。
↙️ 深度优先遍历树
深度优先树遍历是一种通过拾取特定分支来遍历树的算法;并继续向下移动到分支中,直到它到达末端。只有到那时,它才会返回到另一个分支。
在深度优先树遍历的领域内,有几种类型的遍历;其中三种最常见:前序遍历(PreOrder)、中序遍历(InOrder)和后序遍历(PostOrder)。
这些算法是递归的;这意味着它们将在子节点及其子节点上重新开始,依此类推。
在接下来的每个例子中,我们将从下面的二进制树中返回每个节点的值。
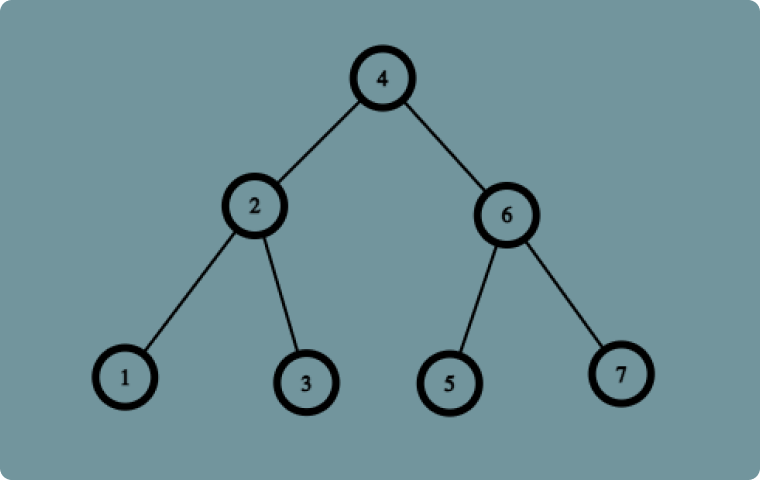
用 PHP 表示该树如下:
$root = [
'value' => 4,
'children' => [
[
'value' => 2,
'children' => [
['value' => 1],
['value' => 3],
],
],
[
'value' => 6,
'children' => [
['value' => 5],
['value' => 7],
],
],
],
];
// Helper function to visualize the visiting of a node.
function visit(array $node): int
{
return $node['value'];
}前序遍历 (节点,左(to),右)
当遍历一棵树时,我们从根节点开始,然后应用算法。
在前序算法中,将首先访问一个节点,然后从左到右访问它的子节点。这个过程是递归的;这意味着它将从它的子节点身上重新开始,等等。
因此,该遍历的输出将为:4、2、1、3、6、5、7。
首先我们访问 4,然后转到它的第一个子(左)节点,并再次应用相同的算法。因此,从该节点中,我们首先访问 2,然后转到它的第一个(左)子节点,并再次应用算法。当我们达到 1 时,我们命中了一个叶节点(Leaf)。它没有子节点,因此没有左节点或右节点的输出。我们已经达到了这个树枝的最大深度。
所以现在我们回溯到前一个节点 2 并完成它的算法。我们向右走:3。此节点也是一个叶子。所以我们回溯到上一个节点:2。现在已经完成;所以我们进一步回溯到 4。我们向右走并访问:6,算法重复:向左走:5;回溯并向右走:7。
示例代码
前序遍历的 PHP 实现:
function preOrder(array $node)
{
// First we visit the node itself.
$output[] = visit($node);
// Then apply the algorithm to every child from left -> right.
foreach ($node['children'] ?? [] as $child) {
$output[] = preOrder($child);
}
return implode(', ', $output);
}
echo preOrder($root); // 4, 2, 1, 3, 6, 5, 7中序遍历(左,节点,右)
中序遍历的算法在二叉树上最有意义。这是因为我们先向左走,然后访问节点本身,然后向右走。如果有3个子节点,我们需要选择如何处理中间节点;befóre 或 áfter 节点本身。
运行此算法将产生以下输出:1,2,3,4,5,6,7。
因为该算法首先访问左节点,所以我们一直向下遍历,直到到达最左侧的节点 1。因为它没有子节点,我们不能再向左走了。因此,我们访问节点本身。我们也不能向右走;所以我们回溯到上一个节点:2。这已经耗尽了整个的左分支,所以我们访问节点本身。然后我们转到右侧节点,并重复该算法…,等等
示例代码
PHP 实现的中序遍历:
function inOrder(array $node)
{
// We extract a possible left and right node for clarity.
$left = $node['children'][0] ?? null;
$right = $node['children'][1] ?? null;
// We'll apply the algorithm on the left node first.
if ($left) {
$output[] = inOrder($left);
}
// Now we visit the node itself.
$output[] = visit($node);
// And apply the algorithm on the right node.
if ($right) {
$output[] = inOrder($right);
}
return implode(', ', $output);
}
echo inOrder($root); // 1, 2, 3, 4, 5, 6, 7后序(InOrder)的名称(很可能)是基于它按升序访问每个节点的事实。但这只适用于所谓的排序二叉树。在这种类型的树中,每个左边的子节点都小于节点本身,右边的子节点大于节点本身。就像我们的示例树一样。
后序遍历(左(to), 右, 节点)
在后序遍历中,我们首先访问节点的子节点(从左到右),然后访问节点本身。由于该算法的递归性,输出将为:1,3,2,5,7,6,4。
由于我们已经对其他算法进行了两次(令人疲惫的)演练,而这一次的过程与前序遍历几乎相同,我将让你自己尝试这一次。
示例代码
后序遍历的 PHP 实现:
function postOrder(array $node)
{
// First we'll apply the algorithm on every child from left -> right.
foreach ($node['children'] ?? [] as $child) {
$output[] = postOrder($child);
}
// Then we visit the node itself.
$output[] = visit($node);
return implode(', ', $output);
}
echo postOrder($root); // 1, 3, 2, 5, 7, 6, 4↔️ 广度优先遍历
在广度优先树遍历中,我们从根节点开始,然后访问子节点。但与深度优先方法不同,该算法不是递归应用的;而是更线性。它是逐级进行的,因此也称为层次遍历(LevelOrder)。该算法通常在树的深度未知甚至是动态的情况下使用。
树层次遍历
层次遍历的算法与前序遍历很相似,不过因为广度优先,实际上在访问下一级子节点前先访问子节点。因此,首先它访问根节点 4,然后是它的子节点:2 和 6,然后才是 2 和 6 的子节点。i
为了正确看待这一点,LevelOrder 层次遍历的输出将是:4,2,6,1,3,5,7。在进入下一个级别之前,每个级别都会被访问。
要实现此行为,可以使用队列。这是一个简单的列表或数组,当访问节点时,我们会将每个子节点附加到该列表或数组中。首先将根节点添加到队列中,然后在访问队列的第一个节点的队列上启动递归函数;将其子项添加到队列中,然后重新开始;直到整个队列为空。
示例代码
层次遍历的 PHP 实现:
function levelOrder(array $queue, array $output = [])
{
// If the queue is empty, return the output.
if (count($queue) === 0) {
return implode(', ', $output);
}
// Take the first item from the queue and visit it.
$node = array_shift($queue);
$output[] = visit($node);
// Add any children to the queue.
foreach ($node['children'] ?? [] as $child) {
$queue[] = $child;
}
// Repeat the algorithm with the rest of the queue.
return levelOrder($queue, $output);
}
// Put the root on the queue.
$queue = [$root];
echo levelOrder($queue); // 4, 2, 6, 1, 3, 5, 7🤔 树遍历用途
如果你和我一样,喜欢学习这样的东西;但也希望/需要一个实际的理由来使用它。所以让我们进一步探讨一下。
注意:对于这个示例,你绝对可以不需要树。就像生活中的大多数东西一样,你可以选择使用它;如果你喜欢的话。
示例:创建文档
假设我们有一个内容管理系统(CMS),用于创建文档(或书本)的章节层次结构。它有如下部分:
- 一个封面 (C)
- 一个目录 (TOC)
- 章节 1~3 并带有一些嵌套的子章节
由于有嵌套和层次结构,你的CMS可能已经有了树状结构。所以,让我们接受这一点,并将其放在一棵树上,如下所示:
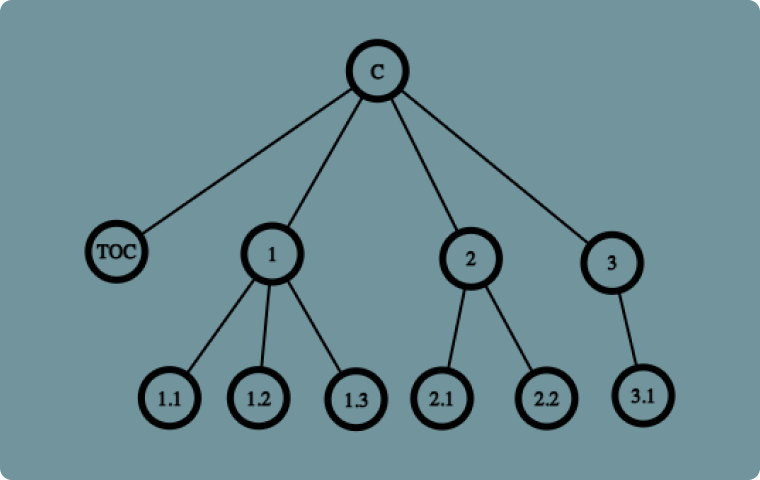
由于树结构需要根节点,我们选择封面作为根节点。它的子节点为目录及各个主章节。主章节也都有其子章节
渲染整个文档(前序遍历)
如果我们想将每个部分组合成一个单一的逻辑流动文档,我们可以使用前序遍历访问节点。为什么?因为我们首先访问节点本身,然后使用深度优先算法从左到右访问其子节点。这意味着输出将是 C、TOC、1、1.1、1.2、1.3、2、2.1、2.2、3、3.1。
使用前序遍历的另一个常见任务是克隆树。由于我们以正确的顺序访问每个节点,因此你可以完整克隆每个节点,并设置正确的父节点(因为它已经存在)。
从树中移除页面(后序遍历)
假设我们不需要主章节 2,但我们确实需要它的子章节 2.1 和 2.2(以及可能的孙子章节)。如果我们使用前序遍历,我们将首先访问主节点。如果我们要删除那个节点;你也会失去所有子节点。为了防止这种情况,我们可以使用后序遍历。由于这基本上是自下而上的,我们可以将2.1 和 2.2 提升一个级别(通过更新父节点),然后安全地删除章节 2。
示例:索引网站(层次遍历)
此例中,我们将索引一个网站。我们的根节点是网站的主页。因为我们不知道会遇到多少链接,我们也不知道树的深度。在这种情况下,最好使用广度优先遍历。因为它一级一级地遍历一棵树;如果这个过程太深,我们可以停止。我们可以设置最大深度。深度优先的方法可能会在分支再次出现之前让你沿着分支深入下去。不理想。
当我们从根节点开始时,我们访问(也称为索引)它。然后我们找到页面上的每个(内部)链接,并将这些页面添加到队列中;并重复该过程,直到队列为空。
为了防止可能的无限循环,因为链接可以在多个页面上并链接回这些页面,你需要跟踪已访问的每个节点,并且只有在尚未访问的情况下才将其添加到队列中。
🔗 有用的链接
📤 PHP有一些使用数据结构的助手类。例如,你可以使用这个 SplQueue 来实现广度优先遍历。
感谢阅读
虽然这篇文章与PHP不是很相关;我认为对树原理和遍历算法有一个基本的了解是很好的。你永远不知道在什么情况下你最终需要这个。

 上一篇
上一篇 
 QQ 空间
QQ 空间
 QQ 好友
QQ 好友
 微博
微博